mysql索引原理01--索引的数据结构
前言
问起mysql索引，基本上所有人都知道索引是用于加快查询速度的。但是为什么索引能加快查询速度？可能很多了解不深的人会答出类似于“索引就像一本书的目录，可以直接根据目录查找到对应的内容”。这么说其实只是说出了最外层的一些理解，最多只是一个比喻的内容。下面来说一下索引实际上是个什么东西，是怎么样实现的。
说到索引，就必须说一下索引的数据结构，mysql的索引使用的是b+树这个数据结构，为什么mysql要使用b+树，而b+树又是什么呢？下面会通过几个数据结构分析一下为什么mysql要这样做。
不过，在讲之前，我们先看下一个例子，我们有5，22，23，34，77，89，91这几个数，假如他们是一个有序的数组，从5到91排列。
那么假如我们现在需要查询91这一个数，想一想，我们需要查询多少次？没错，我们需要从5开始一个一个比对，总共比对7次才能得到我们想要的结果，这个速度过于慢了。我们可以结合这个场景，看下我们接下来要讲的数据结构。
1.二叉树
二叉树是一个比较规则的一个树状数据结构，它的特点是，根节点只会有两个孩子节点，左孩子的值比根节点小，右孩子的值比根节点大，那么如果我们上面的数组，用二叉树会是怎样的情况？如下图所示。
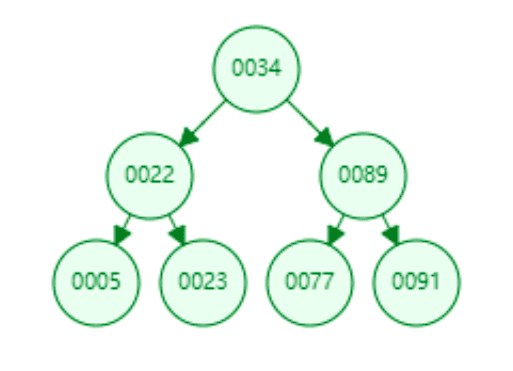那么如果我们要查询91，就可以发现，我们只需要比对三次就可以了，足足快了一半有多！索引其实就是这么用数据结构实现的，具体的结构且看下面。
1.1.结合二叉树分析索引的实现
在索引的实现里面，其实分成了两部分。一部分是索引的二叉树结构存储，索引字段的值都会以二叉树的形式储存，而另一部分是实际的数据表数据。在二叉树的每个节点上都存有一个指向数据表数据的指针。
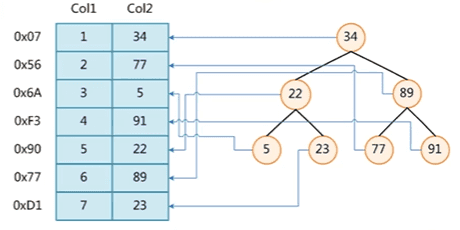既然二叉树这么好，为什么mysql不直接使用二叉树作为索引的数据结构呢？答案是会存在树的深度的问题。刚才的例子，假如我们的二叉树是这样存储的：
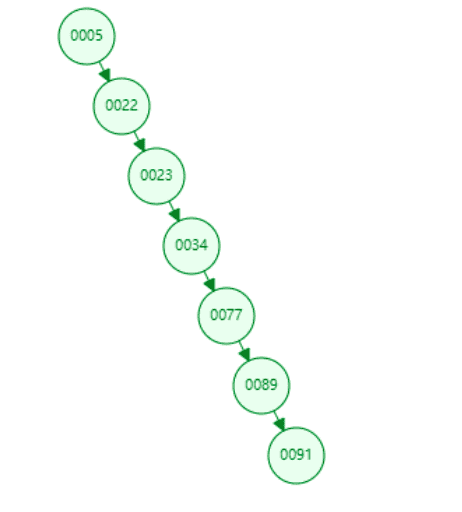那么是不是就很容易发现问题？这棵树深度太高了，和有序数组一样，查询91需要比对7次。所以我们引入了红黑树。
2.红黑树
红黑树简单的来说就是一个会自动平衡的二叉树。只要节点出现单边增长的情况，节点就会自旋，自动平衡成一颗二叉树。比如我们按上面的例子，先插一个5。
然后插入一个22，按照二叉树特性，会成为5的右孩子节点。
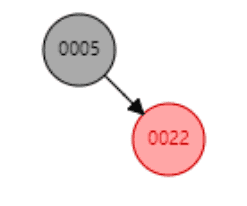最后插入一个23，按二叉树特性，应该会成为22的右孩子节点，但是这里红黑树的特性就体现出来了，因为23成了22的右孩子，就出现了单边增长，所以红黑树发生自旋，22成为了根节点，5成为了左孩子节点，23成为了右孩子节点。
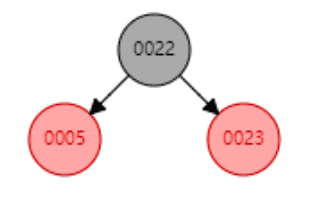可以发现，红黑树完全解决了二叉树单边增长的情况，解决了树深度过高的情况。但实际上这其实也是减缓了而已。细想下，如果数据量达到了千万级别，红黑树深度仍然也是会过深的。那么要怎么解决呢？如果能横向发展，那就能解决深度问题了。没错，b树就是解决这一个问题的。
3.b树
b树是一个平衡的多叉树。它的叶节点都位于同一层，而且索引值仍然保留了从左到右递增的特性。也就是说在红黑树的基础上，增加了同一层多个节点的特性。
同样按照上面的例子，以同一层宽度是4的b树（就是一个大节点可以放四个节点）为例：
先插入一个5
然后插入一个22，可以发现没到最大宽度的时候，22和5是在同一层的，而且在5的右边
再插入一个23，同样到了22的右边
最后插入34，这时已达到最大宽度，b树进行了分裂，22变成了根节点，将5变成了左孩子节点，23和34仍然在一个大节点，变成了右孩子节点
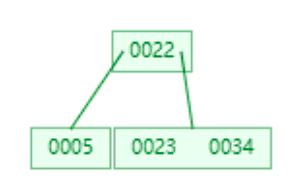如果全部都插入完成，我们会得到这么一个树：
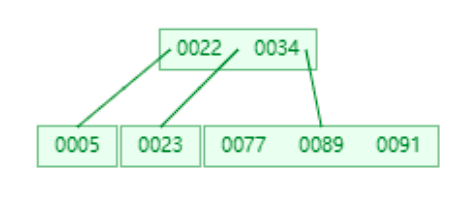可以发现，这棵树比普通的二叉树，红黑树，深度还要小1，即便再多插多个值，深度也会保持增长得很小，一个大节点有4个，那么两行总共可以储存4+5*4=24个值，而普通二叉树两行只能储存3个值。同样的深度，b树很明显能储存更多的值，这很有效的处理了深度过大的问题。而且实际上一个节点储存的远不止4个值。（这里涉及mysql的储存大小问题，这里不赘述，知道有这么回事就行。）
讲到这里，大家已经可以发现，b树基本上已经可以满足大多数的迅速查询的需求了。但是b树仍然存在一个比较大的问题。那就是范围查找的问题。可以想一下，比如我要查询大于5的所有值。糟糕，5的根节点是大于5，根节点的其他子节点也是大于5，这可难找了。于是mysql引入了b+树。
4.b+树
b+树是b树的一种变种，基本上和b树差不多，可以直接看b+树的结构：
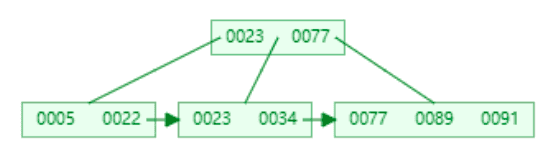基本结构其实大致上是一致的，只是b+树有一点不同的就是会把根节点冗余到叶子节点。然后叶子节点会有从左到右指针相连。大家应该可以发现了，这不就解决了范围查询问题了吗。如果要大于5的，找到5之后，就只需要在叶子节点处一直往右查询就能把所有的查询出来了，这样查询的速度就达到了最快了。这也是mysql采用b+树的原因。
总结
以上就是索引数据结构相关的讲解，下一篇文章将会讲解mysql存储引擎索引的实现。 文中的图都是截自：https://www.cs.usfca.edu/~galles/visualization/Algorithms.html。这个网站可以看各种数据结构的演变过程，包含动画。